Lập trình Pascal: Giải phương trình bậc 2 (ax2+ bx + c =0)

Lập trình Pascal là gì?

Pascal là một ngôn ngữ lập trình mạnh mẽ và phổ biến, cho phép người dùng giải phương trình bậc 2 một cách dễ dàng. Đây là một chức năng rất hữu ích trong việc giải quyết các bài toán toán học và khoa học. Với Pascal, người dùng có thể nhập các hệ số của phương trình và sau đó nhận được kết quả với chỉ vài dòng mã. Điều này giúp người dùng tiết kiệm thời gian và nâng cao hiệu suất công việc của mình.

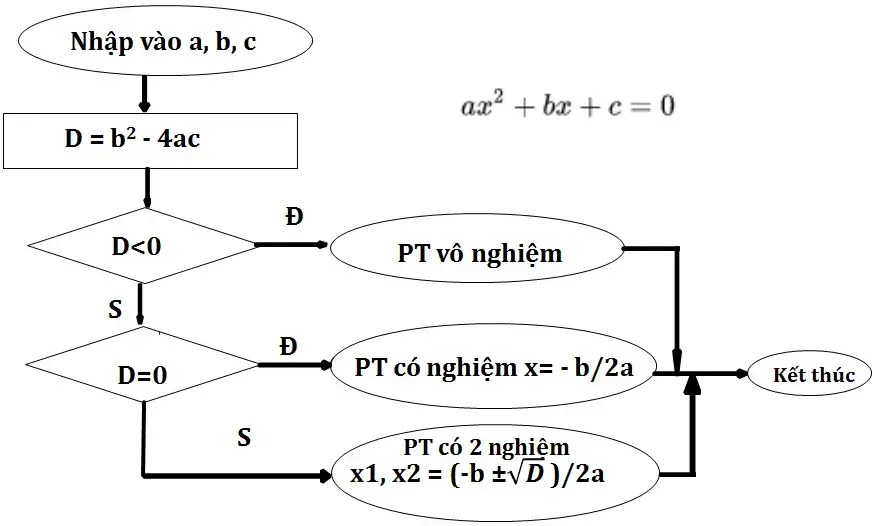
Giải phương trình bậc 2 (ax²+ bx + c =0)

Program GIAI_PHUONG_TRINH_BACII;
Uses CRT; {Su dung thu vien CRT}
Var a,b,c,D,x,x1,x2: real;
Begin
  Clrscr; {xoa man hình, neu khong USES CRT thi lenh nay se bi bao loi}
  Writeln('GIAI PHUONG TRINH BAC II: ');
  Writeln('-------------------------------------------');
  Write('Nhap he so a='); readln(a); {Viet thong bao nhap a vaf cho nhap he so a vao tu ban phim }
  Write('Nhap he so b='); readln(b); {Viet thong bao nhap b vaf cho nhap he so b vao tu ban phim }
  Write('Nhap he so c='); readln(c); {Viet thong bao nhap c vaf cho nhap he so c vao tu ban phim }
  If a=0 then
    If b=0 then
      If c=0 then
        Writeln('Phuong trinh co vo so nghiem') {a=0, b=0, c=0 }
      Else Writeln('Phuong trinh vo nghiem')    {a=0, b=0, c<>0}
    Else Writeln('Phuong trinh co mot nghiem: x=',-c/b: 4: 2)   {a=0, b<>0}
  Else {a <> 0}
    Begin
      D:=b*b-4*a*c;
      If D=0 then Writeln('Phuong trinh co nghiem kep: x=',-b/(2*a): 4: 2) {Delta =0}
      Else
        If D<0 then Writeln('Phuong trinh vo nghiem')                      {Delta <0} 
        Else                                                               {Delta >0}
           Begin
             x1:=(-b-sqrt(D))/(2*a);
             x2:=(-b+sqrt(D))/(2*a);
             Writeln('Phuong trinh co 2 nghiem la x1= ',x1:4:2 ,' va x2= ',x2:4:2); 
           End;
     End;
Readln {Truoc END. thi khong can dau ;}
End. 

Cách phát hiện và xử lý các trường hợp đặc biệt trong việc giải phương trình bậc 2 bằng ngôn ngữ Pascal là gì?

Cách phát hiện và xử lý các trường hợp đặc biệt trong việc giải phương trình bậc 2 bằng ngôn ngữ Pascal như sau:
1. Trường hợp a = 0:
- Nếu a = 0 và b = 0, phương trình trở thành phương trình vô số nghiệm.
- Nếu a = 0 và b khác 0, phương trình trở thành phương trình vô nghiệm.
2. Trường hợp delta (Δ) = 0:
- Delta (Δ) được tính theo công thức Δ = b^2 - 4ac. Nếu Δ = 0, phương trình có nghiệm kép x = -b/(2a).
3. Trường hợp delta (Δ) < 0:
- Nếu Δ < 0, phương trình bậc 2 vô nghiệm.
4. Trường hợp delta (Δ) > 0:
- Nếu Δ > 0, phương trình có 2 nghiệm phân biệt x1 và x2 được tính theo công thức:
x1 = (-b + √Δ)/(2a) và x2 = (-b - √Δ)/(2a).
Trong code Pascal, các bước sau có thể được thực hiện để giải phương trình bậc 2:
1. Nhập giá trị a, b và c.
2. Kiểm tra trường hợp đặc biệt:
- Nếu a = 0, xử lý trường hợp đặc biệt tương ứng.
3. Tính delta (Δ) theo công thức Δ = b^2 - 4ac.
4. Kiểm tra các trường hợp đặc biệt sau:
- Nếu Δ = 0, tính nghiệm kép x và hiển thị kết quả.
- Nếu Δ < 0, hiển thị thông báo phương trình vô nghiệm.
- Nếu Δ > 0, tính nghiệm x1 và x2 và hiển thị kết quả.
5. Kết thúc chương trình.
Chúng ta có thể sử dụng các câu lệnh IF...THEN để thực hiện các kiểm tra trường hợp và tính toán theo công thức cho phương trình bậc 2 trong ngôn ngữ Pascal.
Lưu ý rằng đây chỉ là một cách phân tích cơ bản để giải phương trình bậc 2 trong Pascal. Bạn có thể tùy chỉnh và cải tiến mã nguồn để đáp ứng yêu cầu cụ thể của bạn.