

- Trang chủ
- Lớp 12
- Giải sách giáo khoa lớp 12
- Giải tích lớp 12
- Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số


Giải câu 1 bài 1: Sự đồng biến, nghịch biến của hàm số
Bài 1: Trang 9 - sgk giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số
a) $y=4+3x-x^{2}$.
b) $y=\frac{1}{3}x^{3}+3x^{2}-7x-2$.
c) $y=x^{4}-2x^{2}+3$.
d) $y=-x^{3}+x^{2}-5$.
Bài Làm:
a) TXĐ $D=\mathbb{R}$
Ta có $y'=3-2x \Rightarrow y'=0 \Leftrightarrow x=\frac{3}{2}$
Bảng biến thiên
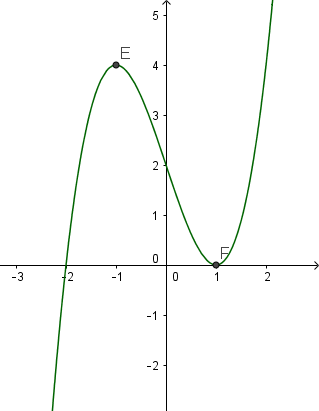
Vậy hàm số đã cho đồng biến trên khoảng $(-\infty, \frac{3}{2})$ và nghịch biến trong khoảng $(\frac{3}{2}, +\infty)$.
b) TXĐ $D=\mathbb{R}$.
Ta có $y'=x^{2}+6x^{2}-7 \Rightarrow y'=0 \Leftrightarrow \left[ \matrix{x=-7 \hfill \cr x=1 \hfill \cr} \right.$
Bảng biến thiên

Vậy hàm số đồng biến trên các khoảng $(-\infty,-7) \cup (1,+\infty)$ và nghịch biến trên khoảng (-7,1).
c) TXĐ $D=\mathbb{R}$
$y'=4x^{3}-4x=4x(x^{2}-1)=0 \Leftrightarrow \left[ \matrix{x=0 \hfill \cr x=1 \hfill \cr x=-1\hfill \cr} \right.$
Ta có bảng biến thiên
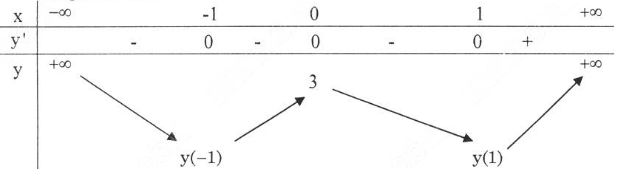
Vậy hàm số nghịch biến trên khoảng $(-\infty,-1) \cup (0,1)$ và đồng biến trên các khoảng $(-1,0) \cup (1, +\infty)$.
d) TXĐ $D=y'=-3x^{2}+2x=0 \Leftrightarrow \left[ \matrix{x=0\hfill \cr x=\frac{2}{3} \hfill \cr} \right.$
Ta có bảng biến thiên
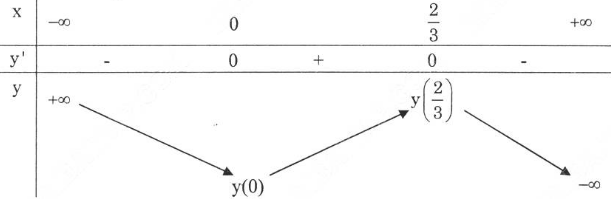
Vậy hàm số đồng biến trên khoảng $(0,\frac{2}{3})$ và nghịch biến trên khoảng $(-infty,0) \cup (\frac{2}{3},+\infty)$.
Danh Mục Tin Tức
- Hướng dẫn
- Mẹo vặt
- Kinh nghiệm
- Xu Hướng
- Cách làm
- Tài liệu
- Hình nền
- Giải bài tập
- Công thức
- Kỳ thi THPT quốc gia
- Văn Học
- Bài Học
- Lớp 12
- Lớp 1
-
Lớp 2
-
Lớp 2 - cánh diều
-
Giải sách giáo khoa
- Âm nhạc 2 - cánh diều
- Giáo dục thể chất 2 - cánh diều
- Hoạt động trải nghiệm 2 - cánh diều
- Mỹ thuật 2 - cánh diều
- Tiếng Anh 2 - cánh diều
- Tiếng Việt 2 tập 1 - cánh diều
- Tiếng Việt 2 tập 2 - cánh diều
- Toán 2 tập 1 - cánh diều
- Toán 2 tập 2 - cánh diều
- Tự nhiên và xã hội 2 - cánh diều
- Đạo đức 2 - cánh diều
- Giải vở bài tập
-
Giải sách giáo khoa
-
Lớp 2 - chân trời sáng tạo
-
Giải sách giáo khoa
- Giải Tiếng việt 2 tập 1 - chân trời sáng tạo
- Giải âm nhạc 2 - chân trời sáng tạo
- Giải hoạt động trải nghiệm 2 - chân trời sáng tạo
- Giải mỹ thuật 2 - chân trời sáng tạo
- Giải tiếng Anh 2 - chân trời sáng tạo
- Giải Tiếng Việt 2 tập 2 - chân trời sáng tạo
- Giải toán 2 - chân trời sáng tạo
- Giải tự nhiên và xã hội 2 - chân trời sáng tạo
- Giải đạo đức 2 - chân trời sáng tạo
- Toán 2 tập 1 - chân trời sáng tạo
- Toán 2 tập 2 - chân trời sáng tạo
-
Giải vở bài tập
- Giải VBT Tiếng Anh 2 - chân trời sáng tạo
- Giải VBT Tiếng Việt 2 tập 1 - chân trời sáng tạo
- Giải VBT Tiếng Việt 2 tập 2 - chân trời sáng tạo
- Giải VBT toán 2 tập 1 - chân trời sáng tạo
- Giải VBT toán 2 tập 2 - chân trời sáng tạo
- Giải VBT Tự nhiên và xã hội 2 - chân trời sáng tạo
- Giải VBT Đạo đức 2 - chân trời sáng tạo
-
Giải sách giáo khoa
-
Lớp 2 - kết nối tri thức
-
Giải sách giáo khoa
- Giải âm nhạc 2 - kết nối tri thức
- Giải hoạt động trải nghiệm 2 - kết nối tri thức
- Giải mĩ thuật 2 - kết nối tri thức
- Giải Tiếng Việt 2 tập 1 - kết nối tri thức
- Giải Tiếng việt 2 tập 1 - kết nối tri thức
- Giải Tiếng việt 2 tập 2 - kết nối tri thức
- Giải toán 2 tập 1 - kết nối tri thức
- Giải toán 2 tập 1 - kết nối tri thức
- Giải toán 2 tập 2 - kết nối tri thức
- Giải tự nhiên và xã hội 2 - kết nối tri thức
- Giải đạo đức 2 - kết nối tri thức
-
Giải vở bài tập
- Giải VBT tập viết 2 tập 1 - kết nối tri thức
- Giải VBT Tiếng Việt 2 tập 1 - kết nối tri thức
- Giải VBT Tiếng Việt 2 tập 2 - kết nối tri thức
- Giải VBT toán 2 tập 1 - kết nối tri thức
- Giải VBT toán 2 tập 2 - kết nối tri thức
- Giải VBT Tự nhiên và xã hội 2 - kết nối tri thức
- Giải VBT Đạo đức 2 - kết nối tri thức
- Giải VBT Hoạt động trải nghiệm 2
-
Giải sách giáo khoa
-
Lớp 2 - cánh diều
-
Lớp 3
-
Lớp 3 - cánh diều
- Giải sách giáo khoa
-
Giải vở bài tập
- Giải VBT toán 3 tập 1 - cánh diều
- Giải VBT toán 3 tập 2 - cánh diều
- Giải VBT toán 3 - cánh diều
- Giải VBT tiếng việt 3 tập 1 - cánh diều
- Giải VBT tiếng việt 3 tập 2 - cánh diều
- Giải VBT đạo đức 3 - cánh diều
- Giải VBT tự nhiên xã hội 3 - cánh diều
- Giải VBT hoạt động trải nghiệm 3 - cánh diều
- Giải VBT tin học 3 - cánh diều
-
Lớp 3 - chân trời sáng tạo
-
Giải sách giáo khoa
- Giải âm nhạc 3 - chân trời sáng tạo
- Giải công nghệ 3 - chân trời sáng tạo
- Giải hoạt động trải nghiệm 3 - chân trời sáng tạo
- Giải mĩ thuật 3 - chân trời sáng tạo
- Giải tin học 3 - chân trời sáng tạo
- Giải toán 3 tập 1 - chân trời sáng tạo
- Giải toán 3 tập 2 - chân trời sáng tạo
- Giải tự nhiên và xã hội 3 - chân trời sáng tạo
- Giải đạo đức 3 - chân trời sáng tạo
- Giải tiếng việt 3 tập 1 - chân trời sáng tạo
- Giải tiếng việt 3 tập 2 - chân trời sáng tạo
-
Giải vở bài tập
- Giải VBT toán 3 tập 1 - chân trời sáng tạo
- Giải VBT toán 3 tập 2 - chân trời sáng tạo
- Giải VBT tiếng việt 3 tập 1 - chân trời sáng tạo
- Giải VBT tự nhiên xã hội 3 - chân trời sáng tạo
- Giải VBT hoạt động trải nghiệm 3 - chân trời sáng tạo
- Giải VBT công nghệ 3 - chân trời sáng tạo
- Giải VBT tin học 3 - chân trời sáng tạo
- Giải VBT tiếng việt 3 tập 2 - chân trời sáng tạo
- Giải VBT đạo đức 3 - chân trời sáng tạo
-
Giải sách giáo khoa
-
Lớp 3 - kết nối tri thức
-
Giải sách giáo khoa
- Giải âm nhạc 3 - kết nối tri thức
- Giải công nghệ 3 - kết nối tri thức
- Giải hoạt động trải nghiệm 3 - kết nối tri thức
- Giải mĩ thuật 3 - kết nối tri thức
- Giải tin học 3 - kết nối tri thức
- Giải toán 3 tập 1 - kết nối tri thức
- Giải toán 3 tập 2 - kết nối tri thức
- Giải tự nhiên và xã hội 3 - kết nối tri thức
- Giải đạo đức 3 - kết nối tri thức
- Giải tiếng việt 3 tập 1 - kết nối tri thức
- Giải tiếng việt 3 tập 2 - kết nối tri thức
- Văn mẫu 3 - kết nối tri thức
-
Giải vở bài tập
- Giải VBT toán 3 tập 2 - kết nối tri thức
- Giải VBT tiếng việt 3 tập 1 - kết nối tri thức
- Giải VBT tiếng việt 3 tập 2 - kết nối tri thức
- Giải VBT đạo đức 3 - kết nối tri thức
- Giải VBT tự nhiên xã hội 3 - kết nối tri thức
- Giải VBT hoạt động trải nghiệm 3 - kết nối tri thức
- Giải VBT tin học 3 - kết nối tri thức
- Giải VBT toán 3 tập 1 - kết nối tri thức
-
Giải sách giáo khoa
-
Lớp 3 - cánh diều
- Lớp 4
- Lớp 5
-
Lớp 6
-
Lớp 6 - cánh diều
-
Giải sách giáo khoa
- Giải Toán 6 tập 1 - cánh diều
- GiảiToán 6 tập 2 - cánh diều
- Soạn Văn 6 tập 1 - cánh diều
- Soạn Văn 6 tập 2 - cánh diều
- Văn mẫu 6 - cánh diều
- Giải Tiếng Anh 6 tập 1 - cánh diều
- Giải Tiếng Anh 6 tập 2 - cánh diều
- Giải Công dân 6 - cánh diều
- Giải Khoa học tự nhiên 6 - cánh diều
- Giải Lịch sử và Địa lý 6 - cánh diều
- Giải Công nghệ 6 - cánh diều
- Giải Âm nhạc 6 - cánh diều
- Giải Tin học 6 - cánh diều
- Giải Giáo dục thể chất 6 - cánh diều
- Giải toán 6 - cánh diều
- Soạn văn 6 - cánh diều
- Giải Mĩ thuật 6 - cánh diều
- Giải Hoạt động trải nghiệm, hướng nghiệp 6 - cánh diều
-
Giải sách bài tập
- Giải SBT ngữ văn 6 - cánh diều
- Giải SBT ngữ văn 6 tập 1 - cánh diều
- Giải SBT ngữ văn 6 tập 2 - cánh diều
- Giải SBT Toán 6 - cánh diều
- Giải SBT Toán 6 tập 1 - cánh diều
- Giải SBT Toán 6 tập 2 - cánh diều
- Giải SBT Khoa học tự nhiên 6 - cánh diều
- Giải SBT Lịch sử và địa lí 6 - cánh diều
- Giải SBT tin học 6 - cánh diều
- Giải SBT công dân 6 - cánh diều
- Giải SBT công nghệ 6 - cánh diều
- Giải SBT tiếng Anh 6 - cánh diều
-
Trắc nghiệm
- Trắc nghiệm KHTN 6 cánh diều
- Trắc nghiệm toán 6 cánh diều
- Trắc nghiệm ngữ văn 6 cánh diều
- Trắc nghiệm lịch sử 6 cánh diều
- Trắc nghiệm toán 6 cánh diều
- Trắc nghiệm địa lí 6 cánh diều
- Trắc nghiệm âm nhạc 6 cánh diều
- Trắc nghiệm mĩ thuật 6 cánh diều
- Trắc nghiệm công dân 6 cánh diều
- Trắc nghiệm công nghệ 6 cánh diều
- Trắc nghiệm hoạt động trải nghiệm 6 cánh diều
- Trắc nghiệm tin học 6 cánh diều
-
Giải sách giáo khoa
-
Lớp 6 - chân trời sáng tạo
-
Giải sách giáo khoa
- Giải Toán 6 tập 1 - chân trời sáng tạo
- Giải Toán 6 tập 2 - chân trời sáng tạo
- Soạn Văn 6 tập 1 - chân trời sáng tạo
- Soạn Văn 6 tập 2 - chân trời sáng tạo
- Giải toán 6 - chân trời sáng tạo
- Soạn Văn 6 - chân trời sáng tạo
- Giải Khoa học tự nhiên 6 - chân trời sáng tạo
- Giải lịch sử và địa lí 6 - chân trời sáng tạo
- Giải âm nhạc - chân trời sáng tạo 6
- Giải trải nghiệm hướng nghiệp 6 - chân trời sáng tạo
- Giải mĩ thuật - chân trời sáng tạo 6
- Giải giáo dục thể chất 6 - chân trời sáng tạo
- Giải công dân 6 - chân trời sáng tạo
- Giải công nghệ 6 - chân trời sáng tạo
- Giải tiếng Anh 6 - chân trời sáng tạo
-
Giải sách bài tập
- Giải SBT ngữ văn 6 - chân trời sáng tạo
- Giải SBT ngữ văn 6 tập 1 - chân trời sáng tạo
- Giải SBT ngữ văn 6 tập 2 - chân trời sáng tạo
- Giải SBT Toán 6 - chân trời sáng tạo
- Giải SBT Toán 6 tập 1 - chân trời sáng tạo
- Giải SBT Toán 6 tập 2 - chân trời sáng tạo
- Giải SBT Khoa học tự nhiên 6 - chân trời sáng tạo
- Giải SBT Lịch sử và địa lí 6 - chân trời sáng tạo
- Giải SBT tin học 6 - chân trời sáng tạo
- Giải SBT công dân 6 - chân trời sáng tạo
- Giải SBT công nghệ 6 - chân trời sáng tạo
- Giải SBT tiếng Anh 6 - chân trời sáng tạo
- Giải SBT hoạt động trải nghiệm 6 - chân trời sáng tạo
- Giải SBT âm nhạc 6 - chân trời sáng tạo
- Giải SBT mĩ thuật 6 - chân trời sáng tạo
-
Trắc nghiệm
- Trắc nghiệm KHTN 6 chân trời sáng tạo
- Trắc nghiệm toán 6 chân trời sáng tạo
- Trắc nghiệm ngữ văn 6 chân trời sáng tạo
- Trắc nghiệm lịch sử 6 chân trời sáng tạo
- Trắc nghiệm toán 6 chân trời sáng tạo
- Trắc nghiệm địa lí 6 chân trời sáng tạo
- Trắc nghiệm âm nhạc 6 chân trời sáng tạo
- Trắc nghiệm mĩ thuật 6 chân trời sáng tạo
- Trắc nghiệm công dân 6 chân trời sáng tạo
- Trắc nghiệm công nghệ 6 chân trời sáng tạo
- Trắc nghiệm hoạt động trải nghiệm 6 chân trời sáng tạo
- Trắc nghiệm tin học 6 chân trời sáng tạo
-
Giải sách giáo khoa
-
Lớp 6 - kết nối tri thức
-
Giải sách giáo khoa
- Giải Toán 6 tập 1 - kết nối tri thức
- Giải Toán 6 tập 2 - kết nối tri thức
- Soạn Văn 6 tập 1 - kết nối tri thức
- Soạn Văn 6 tập 2 - kết nối tri thức
- Giải Toán 6 - kết nối tri thức
- Soạn Văn 6 - kết nối tri thức
- Giải công dân 6 - kết nối tri thức
- Giải lịch sử và Địa lí 6 - kết nối tri thức
- Giải khoa học tự nhiên 6 - kết nối tri thức
- Giải âm nhạc 6 - kết nối tri thức
- Giải tin học 6 - kết nối tri thức
- Giải công nghệ 6 - kết nối tri thức
- Giải tiếng Anh 6 - kết nối tri thức
- Giải giáo dục thể chất 6 - kết nối tri thức
- Giải hoạt động trải nghiệm, hướng nghiệp 6 - kết nối...
- Giải mĩ thuật 6 - kết nối tri thức
- Giải tiếng Anh 6 tập 1 - kết nối tri thức
- Giải tiếng Anh 6 tập 2 - kết nối tri thức
-
Giải sách bài tập
- Giải SBT ngữ văn 6 - kết nối tri thức
- Giải SBT ngữ văn 6 tập 1 - kết nối tri thức
- Giải SBT ngữ văn 6 tập 2 - kết nối tri thức
- Giải SBT Toán 6 - kết nối tri thức
- Giải SBT Toán 6 tập 1 - kết nối tri thức
- Giải SBT Toán 6 tập 2 - kết nối tri thức
- Giải SBT Khoa học tự nhiên 6 - kết nối tri thức
- Giải SBT Lịch sử và địa lí 6 - kết nối tri thức
- Giải SBT tin học 6 - kết nối tri thức
- Giải SBT công dân 6 - kết nối tri thức
- Giải SBT công nghệ 6 - kết nối tri thức
- Giải SBT tiếng Anh 6 - kết nối tri thức
- Giải SBT hoạt động trải nghiệm 6 - kết nối tri thức
- Giải SBT âm nhạc 6 - kết nối tri thức
- Giải SBT mĩ thuật 6 - kết nối tri thức
-
Trắc nghiệm
- Trắc nghiệm KHTN 6 kết nối tri thức
- Trắc nghiệm toán 6 kết nối tri thức
- Trắc nghiệm ngữ văn 6 kết nối tri thức
- Trắc nghiệm lịch sử 6 kết nối tri thức
- Trắc nghiệm toán 6 kết nối tri thức
- Trắc nghiệm địa lí 6 kết nối tri thức
- Trắc nghiệm âm nhạc 6 kết nối tri thức
- Trắc nghiệm âm nhạc 6 kết nối tri thức
- Trắc nghiệm công dân 6 kết nối tri thức
- Trắc nghiệm công nghệ 6 kết nối tri thức
- Trắc nghiệm hoạt động trải nghiệm 6 kết nối tri thức
- Trắc nghiệm tin học 6 kết nối tri thức
-
Giải sách giáo khoa
- Tài liệu & sách tham khảo theo chương trình giáo dục cũ
-
Lớp 6 - cánh diều
-
Lớp 7
-
Lớp 7 - Cánh diều
-
Giải sách giáo khoa
- Giải âm nhạc 7 - cánh diều
- Giải công nghệ 7 - cánh diều
- Giải hoạt động trải nghiệm 7 - cánh diều
- Giải mĩ thuật 7 - cánh diều
- Giải tin học 7 - cánh diều
- Giải toán 7 tập 1 - cánh diều
- Giải toán 7 tập 2 - cánh diều
- Giải khoa học tự nhiên 7 - cánh diều
- Soạn văn 7 tập 1 - cánh diều
- Soạn văn 7 tập 2 - cánh diều
- Giải công dân 7 - cánh diều
- Giải lịch sử và địa lí 7 - cánh diều
- Giải SBT công nghệ 7 - cánh diều
-
Giải sách bài tập
- Giải SBT ngữ văn 7 tập 1 - cánh diều
- Giải SBT ngữ văn 7 tập 2 - cánh diều
- Giải SBT Toán 7 tập 2 - cánh diều
- Giải SBT Toán 7 - cánh diều
- Giải SBT Khoa học tự nhiên 7 - cánh diều
- Giải SBT Lịch sử và địa lí 7 - cánh diều
- Giải SBT tin học 7 - cánh diều
- Giải SBT công dân 7 - cánh diều
- Giải SBT công nghệ 7 - cánh diều
- Giải SBT hoạt động trải nghiệm 7 - cánh diều
-
Giải sách giáo khoa
-
Lớp 7 - Chân trời sáng tạo
-
Giải sách giáo khoa
- Giải âm nhạc 7 - chân trời sáng tạo
- Giải công nghệ 7 - chân trời sáng tạo
- Giải hoạt động trải nghiệm 7 - chân trời sáng tạo
- Giải mĩ thuật 7 - chân trời sáng tạo
- Giải tin học 7 - chân trời sáng tạo
- Giải toán 7 tập 1 - chân trời sáng tạo
- Giải toán 7 tập 2 - chân trời sáng tạo
- Giải khoa học tự nhiên 7 - chân trời sáng tạo
- Soạn văn 7 tập 1 - chân trời sáng tạo
- Soạn văn 7 tập 2 - chân trời sáng tạo
- Giải công dân 7 - chân trời sáng tạo
- Giải lịch sử và địa lí 7 - chân trời sáng tạo
- Giải SBT ngữ văn 7 tập 1 - chân trời sáng tạo
- Văn mẫu 7 - chân trời sáng tạo
- Trắc nghiệm công dân 7 - chân trời sáng tạo
-
Giải sách bài tập
- Giải SBT ngữ văn 7 tập 1 - chân trời sáng tạo
- Giải SBT ngữ văn 7 tập 2 - chân trời sáng tạo
- Giải SBT toán 7 tập 1 - chân trời sáng tạo
- Giải SBT toán 7 tập 2 - chân trời sáng tạo
- Giải SBT khoa học tự nhiên 7 - chân trời sáng tạo
- Giải SBT lịch sử và địa lí 7 - chân trời sáng tạo
- Giải SBT công nghệ 7 - chân trời sáng tạo
- Giải SBT tin học 7 - chân trời sáng tạo
- Giải SBT công dân 7 - chân trời sáng tạo
- Giải SBT hoạt động trải nghiệm 7 chân trời sáng tạo bản 2
-
Giải sách giáo khoa
-
Lớp 7 - Kết nối tri thức
-
Giải sách giáo khoa
- Giải âm nhạc 7 - kết nối tri thức
- Giải công nghệ 7 - kết nối tri thức
- Giải hoạt động trải nghiệm 7 - kết nối tri thức
- Giải mĩ thuật 7 - kết nối tri thức
- Giải tin học 7 - kết nối tri thức
- Giải toán 7 tập 1 - kết nối tri thức
- Giải toán 7 tập 2 - kết nối tri thức
- Giải khoa học tự nhiên 7 - kết nối tri thức
- Giải công dân 7 - kết nối tri thức
- Soạn văn 7 tập 1 - kết nối tri thức
- Soạn văn 7 tập 2 - kết nối tri thức
- Giải lịch sử và địa lí 7 - kết nối tri thức
- Văn mẫu 7 - kết nối tri thức
- Trắc nghiệm lịch sử 7 - kết nối tri thức
- Trắc nghiệm công dân 7 - kết nối tri thức
- Trắc nghiệm toán 7 - kết nối tri thức
-
Giải sách bài tập
- Giải SBT ngữ văn 7 tập 1 - kết nối tri thức
- Giải SBT ngữ văn 7 tập 2 - kết nối tri thức
- Giải SBT toán 7 tập 1 - kết nối tri thức
- Giải SBT toán 7 tập 2 - kết nối tri thức
- Giải SBT khoa học tự nhiên 7 - kết nối tri thức
- Giải SBT lịch sử và địa lí 7 - kết nối tri thức
- Giải SBT công nghệ 7 - kết nối tri thức
- Giải SBT tin học 7 - kết nối tri thức
- Giải SBT công dân 7 - kết nối tri thức
- Giải SBT hoạt động trải nghiệm 7 - kết nối tri thức
-
Giải sách giáo khoa
-
Lớp 7 - Cánh diều
- Lớp 8
- Lớp 9
- Lớp 10
- Lớp 11
Tin Tức Mới
-
Nghị luận về câu tục ngữ "Ăn quả nhớ kẻ trồng cây"
Tháng Hai 16, 2024 -
Các mẹo thi 120 tình huống mô phỏng đạt điểm tối đa
Tháng Ba 7, 2024 -
Có Chí Thì Nên: Ba Bài Văn Mẫu Nghị Luận về Tư Tưởng Đạo Lý
Tháng Hai 17, 2024

http://baikiemtra.net/uploads/logo-baikiemta_1.png N/A
Lớp học baikiemtra.net
Liên kết nhanh
Subscribe
© Bản quyền thuộc về Hệ thống đề thi, bài kiểm tra, thi thử miễn phí. Thiết kế bởi Bài kiểm tra.,JSC.









Ý kiến bạn đọc